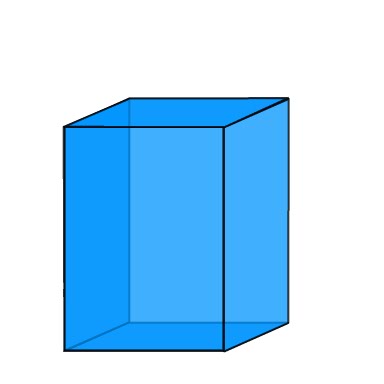
Hexagonal Prism
A one stop resource
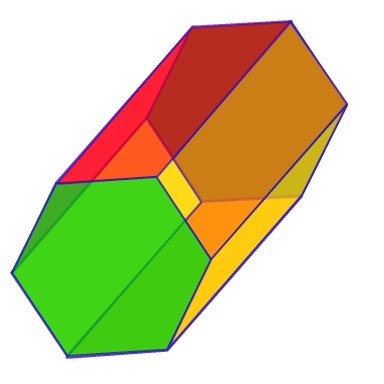
The hexagonal prism is, like the pentagonal prism, not a commonly studied prism at elementary level.
Except for identification, an elementary student is most likely not going to be expected to perform calculations regarding this 3d shape. However, just in case, I have included it in this section for your use.
The most common every day example of a hexagon I have seen is traffic sign posts (some are of course pentagons and octagons). Of course these are three dimensional, but appear to be two dimensional flat shapes to most kids. An excellent, obviously three dimensional object, are nuts from a nuts and bolts set!
The Facts
|
Image |
 |
|
Cross Section |
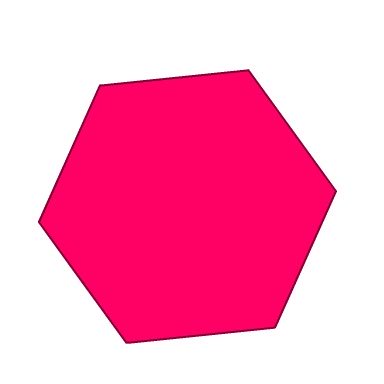 |
|
Faces |
EIGHT - The front and back faces (2) which are hexagons, and six rectangles (6) which connect them. |
|
Vertices |
12 Vertices |
|
Edges |
18 Edges |
|
Surface Area |
 Where: l = distance from front face to back face |
|
Volume |
 Where: l = distance from front face to back face; B = Area of Base |
|
Area of Hexagon |
 Your student is not expected to know or use this formula, I have put it here for interest purposes only.  If your child is expected to find the area of a Hexagon, it will be by calculating the area of triangles, when they are given the value of the Apothem. Click the button below to get a full explanation of this method. |
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.