The Volume of Prism Shapes
Explained Fully
The volume of prism shapes - ANY PRISM is simply the area of its base multiplied by the length of the prism. That is it for EVERY and ANY prism. But the question most curious elementary students will ask is "why?"
If this is the point your child is at, then you are in the right place to get exactly the information you need to explain it. Of course your child should fully understand what area, surface area and volume are; and know how to calculate area of 2D-shapes to get the most out of this section.
Before We Start
Let's be sure we fully understand what the definitions of 'volume' and 'prism' are.
Definition of Volume
This is the amount of space contained within a three dimensional shape.
Definition of Prism
This is a three dimensional shape, where the front and back faces are two identical polygons, and both polygons are connected by parallel lines. These parallel lines will ensure that a cross section ANYWHERE on the prism will yield the same identical polygon.
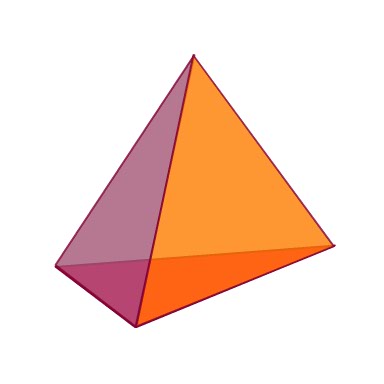
The Triangular Prism
I am going to use the triangular prism as my example to explore the origins of the volume of a prism formula.
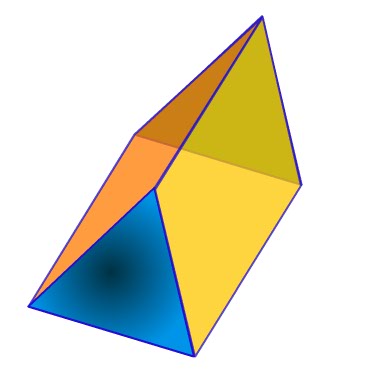
Step 1 |
First we start with just a 2d triangle. It is important, though it is a difficult concept to grasp, that this shape is just what is inside its perimeter. It has NO DEPTH. |
Step 2 |
We must now try to imagin stacking this same shape to make the prism. |
Step 3 |
If we continue this 'stacking' method, we really start to see the triangular prism take shape. In fact, all these shapes stacked one behind the other will create a length - the length of the prism. |
Step 4 |
If we add the area of all these triangles together we will in fact get the volume of the prism. However there is one problem. Since we do not know 'how many' triangles fit into the prism we cannot take this approach. But .... we do know, that no matter how many triangles there are, they will always add to the length of the prism. |
Conclusion |
And this is true for EVERY PRISM whether it is created by a regular or irregular polygon. Where B = Area of Base and l = Length of Prism |
I hope you enjoy this section. If you have any comments or suggestions, on how I can make this geometry resource better for you please don't hesitate to contact me.
Return from thisVolume of Prism to our main prism section to explore prisms in more depth.
or
Return to our k6 geometric shapes home page to explore more great basic geometry.
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.