The Surface Area of a Prism
Fully Explained
To calculate the surface area of a prism is not difficult, once your child understands where the formula comes from.
In this section, I give you the information and the tools to make explaining it to any student as easy as possible.
If you are looking for other information - you will find an entire section on prism here.
I will take the three most common prisms studied at the elementary level and expand upon each one. These are the:
Once these are understood, the principles can be applied to ANY prism.
Surface Area
Before we start, let's be sure we fully understand what the 'surface area' is.
Definition of Surface Area: This is the sum total of areas of ALL the 2D-shapes used to create the OUTSIDE surface of a three dimensional figure.
So the most important skill for a student to develop is the ability to 'see' the shapes that create the surface area of a prism. The best way to show a child these shapes is to actually get them to make and then dismantle 3D-shapes.
For my purpose here, however, I am going to use 3D nets - these are two dimensional representations of the surface of a 3D-Shape.
The Three Most Common Prisms
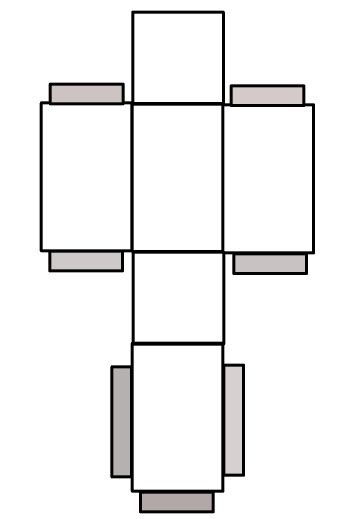 Fig. 1 |
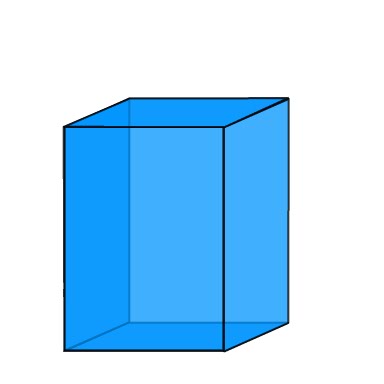
Lets Start with the Cuboid or Rectangular Prism. We can see from its net in Fig.1 that when this prism is opened flat (the grey tabs are simply for construction purposes) it is composed of two identical rectangles - these are the front and back faces of the prism and four other rectangles, which connect the front and back face. Be careful with these other four rectangles, they may be the same size (if the front and back faces are squares) or they may come as two pairs of the same sized rectangles, such as in the image bellow. So the surface area here will be:  |
 Fig.2 |
The Triangular Prism From the net in Fig.2 we can see that this shape is composed of two triangles which are the front and back face, and three rectangles which connect the triangular faces. The surface area of this shape will be: 2 times the area of the triangle + 3 times the area of the rectangles whose dimensions will always be the length of the prism and the length of one side of the triangle.  |
 Fig. 3 |
The Pentagonal Prism From the net in Fig.3 we can see that this prism is composed of seven faces. Two pentagons, and five rectangles. If the pentagons are regular (i.e. have five equal sides and five equal angles) then the surface area of this shape will be: Two times the area of the pentagon plus five times the area of a rectangle with dimensions the length of the prism and the side length of the pentagon. 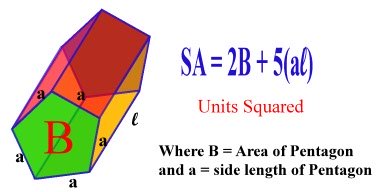 |
Have you noticed the pattern?
A pattern is starting to emerge here, when the face of the prism is a Regular Polygon.
The surface area will ALWAYS BE:
2 x (Area of Regular Polygon Face) + [(number of sides of regular polygon) x (Length of Prism)]
Now to get some practice. Download as worksheets as you need.
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.