Volume of a Sphere Formula
Established from the basics

Your child is so excited! The volume of a sphere formula was introduced to them by their teacher at school. The excitement of being able to deal
with the complicated formula is wonderful, but ...... they asked their teacher where the formual comes from .... and they were told, it would be something
they just have to accept for now. This answer confused your child a little. Why should they have to 'accept' this formula when every other formula has been explained in such detail.
Unfortunately, spherical geometry is exceptionally complicated, and in general requires calculus to develop any proofs. But this doesn't help your child.
They cannot just accept the formuals. So they have come to you, their constant source of knowledge - you have no idea how to explain it, so you have come to the internet - your
constant source of knowledge. Well you are in the right place! On this page, not only are you given the formula you need, but I also take you step by step
with very clear diagrams, through the process of establishing the formula for the volume of a sphere! So let's go.
Volume of a Sphere from first principles.
The volume of a sphere relies on an understanding of the Area of the sphere explanation. In this section I assume you have already read and understood this.
 |
Establish the volume of a sphere with radius r |
Step 1 |
Know, understand and accept that the Surface area of a sphere is:  |
Step 2 |
Here, imagine creating tiny squares all over the surface of the sphere. Then connect the corners of the squares, to the center point of the sphere. These lines and squares now become a square pyramid 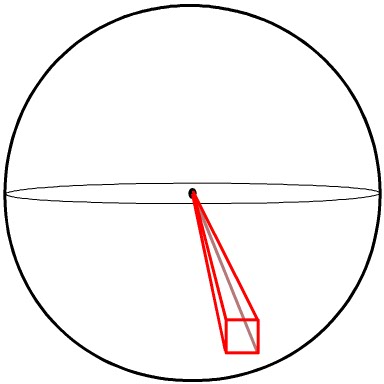 |
Step 3 |
We know that the volume of a pyramid with any base is:  |
Step 4 |
Since we have covered the ENTIRE sphere with these tiny squares, we know that if we add the areas of all the square pyramid base's together we will get the surface area of the sphere, which is:  We also know that the perpendicular height of these pyramids is the radius of the sphere - r. |
Step 5 |
Volume of a pyramid = 1/3 multiplied by Base Area multiplied by height.
Volume of Sphere = 1/3 multiplied by Surface Area of sphere multiplied by Radius of Sphere. Volume of Sphere = 1/3 multiplied by Surface Area of sphere multiplied by Radius of Sphere. VS = (1/3) x (4Pir2) x r VS = (4/3)Pir3 |
 |
Please be aware that I have made many assumptions here, mostly with developing the surface area of the sphere. There are many, many
curves that have not been dealt with properly in this mathematical proof. It's only intention is to give you a firm grasp of the knowledge
behind evaluating the volume, so that your elementary student doesn't just have to accept the formula, but that they can understand how it was developed.
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.