Surface Area of a Sphere Formula
Established from the basics

If your child is not willing to just accept the surface area of a sphere formula as is, then you are in the right place! Congratulations also, as a sure sign
of a budding mathematician is the lack of willingness to accept things but requiring solid proof. If this is what you are seeking
then it is exactly what you are going to get on this page.
In this section, I take you through an easy step by step process, showing you how you can explain the surface area of a sphere to your elementary math student.
Each step will take you closer to establishing the formula, all by yourself.
Surface Area of a Sphere from first principles.
The surface area of a sphere usually requires calculus to be explained. Here I will use basic mathematics methods, to give an intuitive approach, so that your elementary math student will understand where the concept comes from. I do also want to state here that the famous Greek mathematician, Archimedes, was the first to establish this concept.
Step 1

For this proof we will use a sphere with radius r.
In the diagrams, I will use the color blue to show construction lines, and the color red to indicate the math side of things.
Step 2

I want you to picture cutting the sphere into rings of equal height. You can see that each of these rings has a sloped surface.
Step 3

We can now see that, if we ignore the curve of the sphere, and look at the 'red' lines I have drawn; then each ring is like a cross section of a cone (a frustom of a cone).
So here is a big jump. Let's do this.
From now on, we will ignore the curve of the sphere, and just deal with straight lines!
Step 4

Here I have exploded the image of just one of the rings, so that you can see that l is the slant height of the frustom,<i><b> C is the circumference of the sphere, and h is the perpendicular height of the ring we 'cut' in the sphere.
The Surface area of this piece (this ring) is its slant height l multiplied by its length - the circumference of its base- C.
Step 5

In Fig.5 I show the very top ring, and the ring at the center circle of the sphere. You can see, that l gets longer as we get closer to the top or bottom of the sphere, and of course the radius we have called x.
We can actually establish a ratio here between the variables.
This unfortunately is the one thing I am going to say your child 'has to accept'. The proof of this ratio is simply beyond basic math, and the focus of this web site.
Step 6

We can use this ratio, to get a value for l in terms of all other values. Why do we want to do this? Well ... we know that the
surface area of any ring in this sphere is
C x l
We also know that the Circumference of any of these rings (in fact any circle) is
2xPixr
and we also know that every ring in this sphere that we created has a radius we are naming x.
Step 7

In Fig.7 we establish a formula for the surface area of ANY and ALL rings of our sphere. It is:
2 Pi r h
Does this look familiar? It should, it is in fact the formula for the Surface Area of a cylinder with radius r and height h!<br><br>
Step 8
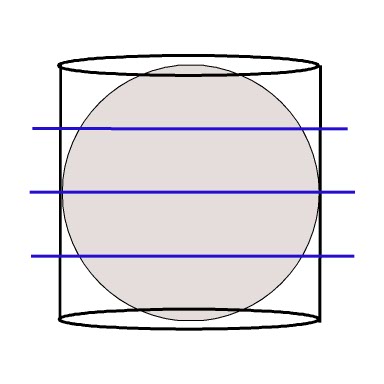
Now imagine our sphere put into a cylinder with radius r, and height 2r. This cylinder circumscribes the sphere.
Now look at the cuts that we originally made to our sphere.
We have established that the surface area of each ring, is in fact the same as the surface area of the cylinder which surrounds it.
If we stack ALL our rings, no matter how many on top of each other, we will get a height of the cylinder 2r.
The height of this cylinder is 2r.
Surface Area of Cylinder = Surface Area of Sphere
Surface Area of Cylinder = 2 Pi r h
h = 2r
Surface Area of Cylinder = 2 x Pi x r x 2r
Surface Area of Cylinder =
4Pir2We established that the surface area of a sphere is equal to the surface area of the cylinder that circumscribes it, so ....

Establishing the Surface area equation, is the first stage of establising the Volume of a Sphere which makes for some very interesting reading also!
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.