Volume of a Pyramid
Explained for the Curious Elementary Math Student

The formula for the Volume of a Pyramid, is all your student NEEDS to know. However for some students this is simply not enough. Sometimes a student WANTS to know where it comes from. This page is for those students. Here, I will show, step by step how this formula came about.

The Volume of a Pyramid from First Principles

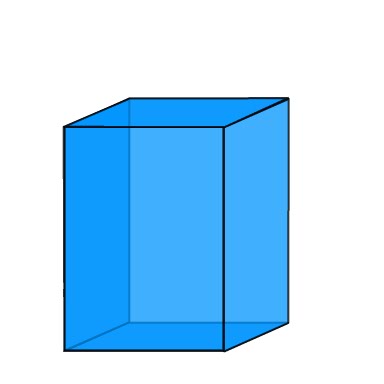
We must first take a look at the properties of Triangular Prisms.

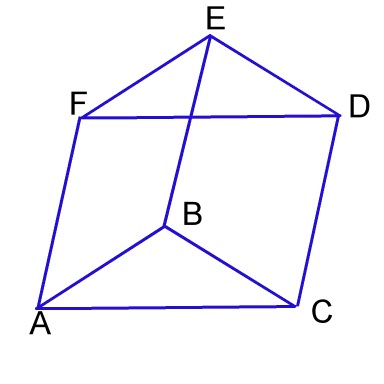Look at the image to the left. This is a Triangular prism with Base ACDF and two triangles, ABC and EFD.

For our purposes here, I will refer to its base as B and it has a height as h.

This prism can be cut into three different pyramids that DO NOT OVERLAP. It can also be shown that these pyramids have the same volume.

This tells us that each pyramid, within the Prism whose volume is its base multiplied by its height is Bh. If the three pyramids are of equal volume, then the volume of each pyramid is Bh/3

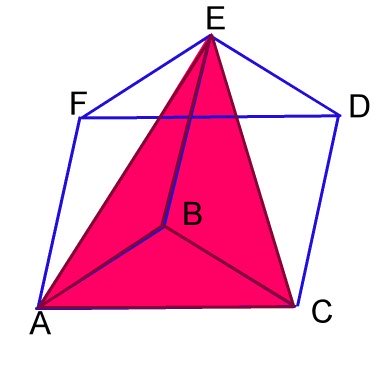This pyramid has base ABC and vertex E.

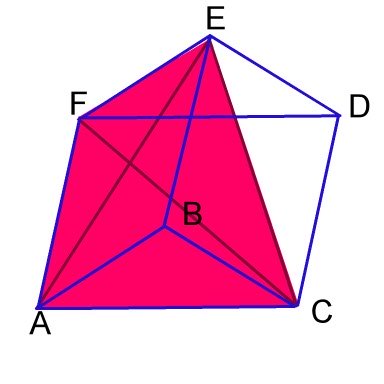This pyramid has base ACF and vertex E.

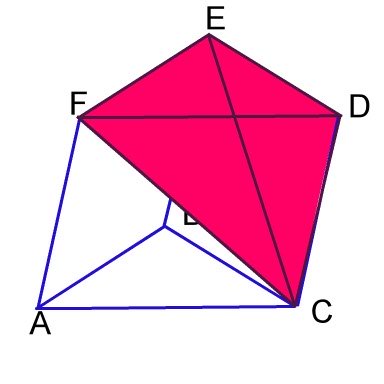This pyramid has base FDC and vertex E.

Every pyramid, is EXACTLY one third the volume of a triangular prism with the same base and height - so...

the volume of ANY Pyramid is .... (Area of its Base x height) divided by three.

Don't forget to check out all the different types of pyramids.

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!

I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.

Be sure to explore everything on this site starting at the home page.