The Pentagon Shape, from recognition to construction.

The Pentagon Shape is one of the shapes your Kindergartner learns to identify as part of their math curriculum. But what catches most elementary students out at some point are the two terms - Pentagon and Regular Pentagon. I feel the reason for this is that the shape above is a Regular Pentagon, but most kids learn to identify it as simply a Pentagon. Is this wrong? No. It is a Pentagon. But a Pentagon is ANY shape composed of 5 intersecting lines.
A regular pentagon is a 5 sided shape where ALL lines are the same length and ALL angles are equal in size.
You can investigate Regular Polygons in a little more detail another time.
The seven steps detailed bellow take you from basic identification all the way through to taking a detailed look at the theorems involving the pentagon shape.
These steps also include 'pit stops' to complete fun geometry projects and coloring sheets.
These are nice 'breathers' on the learning curve, but they are excellent ways of reinforcing the new knowledge in ways that your kid can get a real life, hands on approach to understanding the basic geometry concepts included.
Okay, so let's get started ...
 |
Identify - How do we know what we look at is a Pentagon Shape? |
A Pentagon Shape is identified by the number of sides it has.
It has FIVE sides.
The regular Pentagon is the Pentagon Shape that is studied by students at the elementary level.
A Regular Pentagon is identified by a combination of the number of sides to the shape, the length of the sides AND the size of its angles.
A Regular Pentagon has Five Sides equal in length ... and Five Angles equal in size (all are 108 degrees).
Once your child is comfortable with how to recognize the pentagon shape, offer them a pentagon shape worksheet or two, to see how they get on with identifying it.
 |
Calculate Area & Perimeter of a Regular Pentagon |
To find the area of a Regular Pentagon we must know two things:
1: The length of one side
2: The perpendicular distance from the center of the pentagon to one of its sides. (In 'math speak' this perpendicular distance is known as the APOTHEM!) In my diagram I have included 2 (there is a total of 5 in a pentagon) and these are the blue lines. You can also see that these Apothem's are in fact the radius of a circle inscribed in the pentagon (constructed in green).
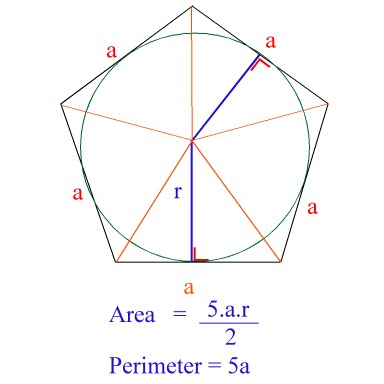
The Area of the pentagon is calculated by first finding the area of one of the Isosceles Triangles created by one side of the pentagon, and two lines constructed from the center point to each vertex. Then you multiply this answer by 5, as there are five of these triangles in a pentagon.
These construction lines are in Orange in my diagram.
Step 1: Area of Isosceles Triangle
Area of any triangle is half its base multiplied by it perpendicular height. In this case
1/2 a r
Step 2: Multiply by 5
We have 5 of these triangles in the Pentagon, so to get the area of the pentagon, we must get the area of ALL five triangles.
5 (1/2 a r)
5/2 a r
These questions can be presented in many different ways, depending on the grade level of your child. For example, if your child is just learning about area (perhaps second or third grade) they could be given the area of one of these triangles. To solve this, they would simply multiply the area given by 5. If on the other hand, your child is in 4th grade, they will probably be given a question which has a solution similar to the explanation above.
But what about a 6th grader? These students could possibly be given information that will require a more complicated solution. And complicated solutions demand an understanding of what is happening, not just a 'plug and play' system with a formula. For example, they could be given the above question, but instead of being given the value of 'r', perhaps they are given the value of the orange construction lines! What then? Would your student see the 10 right angled triangles, rather than the 5 isosceles? Would they make the connection to the Theorem of Pythagoras to find the length of 'r'?
These are good examples of how a shape can be studied all the way through 7 grades, and still get more and more difficult. The difficulty isn't 'tricks' putout there to make a child's life miserable, they are there to ensure a solid understanding. The only way any student can gain this level of understanding is through practice.
The Perimeter of ANY shape is simply the sum total of all the lengths of the shape - and a pentagon is no different.
 |
How to Construct Pentagon ShapeTo complete this, you will need a ruler, pencil, protractor and a blank piece of paper! |
Step 1: Draw a straight line lightly using your ruler and pencil on your paper. - This is what we call a construction line.
Step 2: Indicate on this line, one point - this point will be the first of the five vertices.
Note: We know that the five interior angles of any regular pentagon are equal to 108 degrees.
Step 3: Using your protractor, find the point you decided upon in step to, and measure 108 degrees. Construct a line through your point at 108 degrees.
You now have two lines of your pentagon.
Step 4: Using your ruler, measure the length of your pentagon side on BOTH of these lines, and mark.
Step 5: Using these new points, repeat Step 3: until you have completed your pentagon shape.
Step 6: Your pentagon is the shape contained between the five points of intersection of these five lines.
Step 7: Using a heavier line connect the five points to finish your construction.
A quick check to ensure your pentagon is accurate, is to measure all side lengths with your ruler. If you have done it correctly all sides will measure the same!
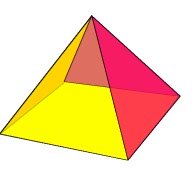 |
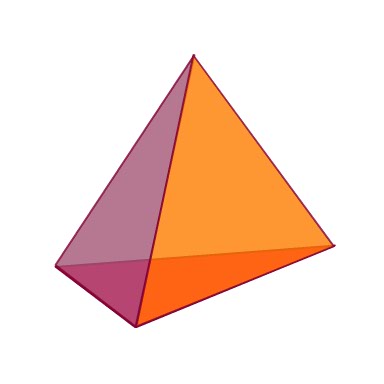
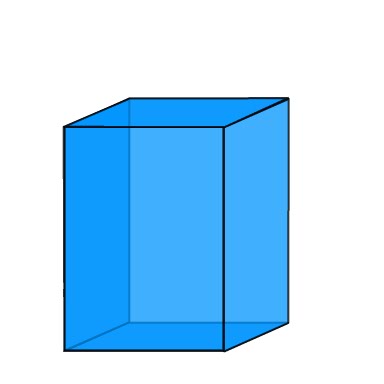
Relationship to 3D Shapes |
The 3d Figures a Kindergarten through sixth grade student is most likely to deal with are the Pentagonal Pyramid and Pentagonal Prism.
They will also be introduced to the Dodecahedron, one of the five platonic solids, which is a three dimensional shape constructed using only regular pentagons. Please be aware, that your student will only be introduced to these, but will NOT have to have the ability to perform any calculations (except perhaps surface area).
 |
Geometric Coloring Sheets |
The use of coloring sheets allows your child to start experimenting with triangles. A great first step is to encourage your child to color in triangles adjacent to each other with the same color, until their shape starts to look like 'something'.
Perhaps that something will be a rectangle or a house! By doing this, your child will start to realize the connection between different shapes. You will find some nice free geometric coloring pages to download and get started with.
 |
Fun Geometry Projects |
Coming soon!
 Pythagoras |
Theorems & Proofs |
Coming soon!
I have created Free printable shape worksheets for you to offer your child for more practice. Download, print and give them to your kids. They're available 24/7!
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.
Return from this Pentagon Shape page to our Regular Polygons Section.
Or
Return from this page to K6 Geometric Shapes Home Page, to explore all the other great sections I have to offer.