The Volume of a Cylinder
Made Easy
The volume of a cylinder is the second thing your child needs to be able to calculate in K-6 Geometry in relation to the cylinder. The first being the Surface area of a cylinder, which I deal with in a different section.
Your child should be comfortable with what volume is, as well as dealing with calculations involving the digits of Pi, to make sense of this section.
What is Volume - a quick recap.
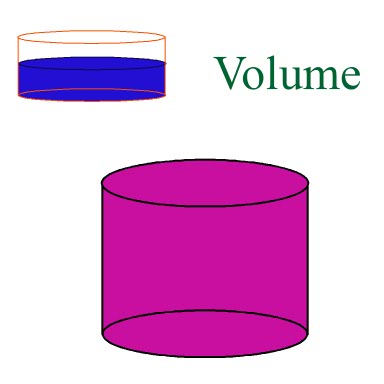
The volume of a container is it's capacity. How much of a substance it can contain. For simplicity, I use the example of water. Now I want to bring your attention to the biggest 'trick' in K-6 volume questions. There CAN BE a difference between the volume of a container, and the volume of water in a container. In the picture above there are two cylindrical containers.
If asked for the volume of the container you use the height of the container for calculations.
If asked for the volume of water in a container, you use the height of the water (the container may not be filled to the top!).
This is about the only 'trick' you need to watch out for!
Volume of a Cylinder

The volume of a Cylinder, like any other prism, is simply its base shape (in this case a circle) stacked upon itself over and over until the given height of the cylinder is achieved.
So how does this help us with our calculations?
Actually a great deal.
We know a circle has no height. It is a 2D shape.
However, the space within a circle (its area) can be calculated. Because a circle has no height, we cannot say HOW MANY CIRCLES go into making a cylinder, we call it an infinite number.
However, no matter how infinite the number of circles, when they are all stacked upon themselves they make the height of the cylinder.
This is why the volume of a cylinder is:
(The area of its base circle) x (Height)
V = Pir2h

Return from volume of a cylinder to our 3d Geometric Shapes section or
Explore K6-Geometric-Shapes more.
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.