Surface Area of a Pyramid
How the Formula is Established

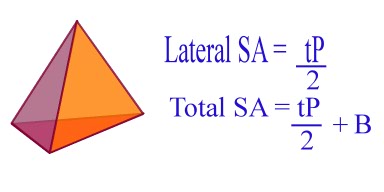
The surface area of a pyramid is not so difficult to establish once your student has a clear understanding of what is going on.  On this page, I will show you, every step of the way, what happens to arrive at the above formula.

It is important to know that there are in fact TWO surface area formulas for the pyramid.

The Lateral Surface Area (which is the surface area of the sides of the pyramid)

The Total Surface Area (the lateral surface area plus the base area).

I will start with the first, establish that, and then the second is merely a 'tag on'!


Before we move forward, be sure your child knows how to label the different parts of a pyramid.


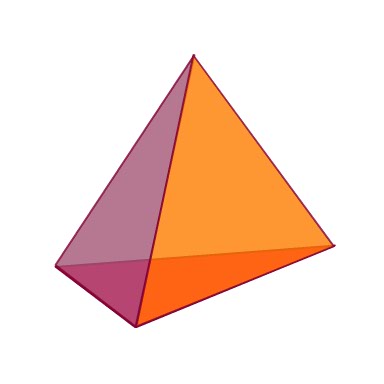
For the purpose of making this section as easy as possible, I am going to use the Right Square Pyramid to illustrate each step.

The square pyramid is named after the base which it rests upon, which is a square. 

My example will be a Right Pyramid, as its vertex is directly above the center point of its base.

Lateral Surface Area of a Pyramid

We are first going to take a look at the triangles that make up the lateral surface of the Pyramid.

These are all isosceles triangles.

We also know that the base of each triangle, is one side of the square base.

If we open the pyramid at it's vertex, and reposition the triangles to be vertical, we can clearly see that the slant height (t) is in fact the perpendicular height of the triangle.

We also know that the

AREA OF A TRIANGLE

is

1/2 the Base by the perpendicular height.

The perpendicular height is t Area of triangle =

(t x triangles base)/2

For this specific Pyramid, if we multiplied the Area of one Triangle by 4 we would have the surface area of a square pyramid - but a formula is only useful if it applies to ALL pyramids.

For this to happen, instead of giving a specific number of sides, we introduce a little Basic Algebra, and say,

ANY PYRAMID would have 'n' triangular faces.

We can now rewrite the Lateral Surface area formula as:

Lateral Area of Pyramid = (t x triangles base x n)/2

In math WE ALWAYS try to reduce a formula down to its simplest form. If we look closely at this formula, we can see that we are not quite done.

If we multiply the triangles base by the number of sides of the polygon which makes the base of the pyramid, we will in fact calculate the Perimeter of the polygon (which is the base). So we can rewrite the formula again in a simpler manner:


LSA = (t x P)/2

Now for the TOTAL SURFACE AREA OF ANY PYRAMID

This is simply the Lateral Surface Area + Base Surface Area


TSA = (t x P)/2 + B

Enjoy this page? Please pay it forward. Here's how...

Would you prefer to share this page with others by linking to it?

  1. Click on the HTML link code below.
  2. Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!

I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.

Be sure to explore everything on this site starting at the home page.