Surface Area of a Cone
Explained for the Curious Elementary Math Student

The formula for the Surface Area of a cone, is all your student NEEDS to know. However for some students this is simply not enough. Sometimes a student WANTS to know where it comes from. This page is for those students.
Here, I will show, step by step how this formula came about.
It is not necessary, however your child may find having both a cone net and a pyramid net helpful while looking at the section.
Surface Area of a Cone from First Principles
We must first take a look at the properties of regular polygons and the circle which circumscribes them.
 |
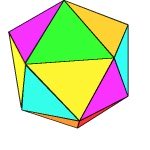
Look at the image to the left. You can see that the surface area of the polygons perimeter is close to the length of the circumference of the circle, but not close enough; so ... |
 |
...let's change the hexagon to a 10 sided polygon - dodechedron. We can see that a polygon perimeter closer still to the circumference, but still not exactly the same; so we will change the number of sides of the polygon again ..... |
 |
...we will now give it 30 sides. You can see that we are now SUPER close to the perimeter of the circle, (not fully there yet) but if we allowed the number of side of the polygon to just continue to increase, we will get closer and closer to the circle. This type of math (to get it exactly right) would involve calculus - which I am not going to explore with you now. |
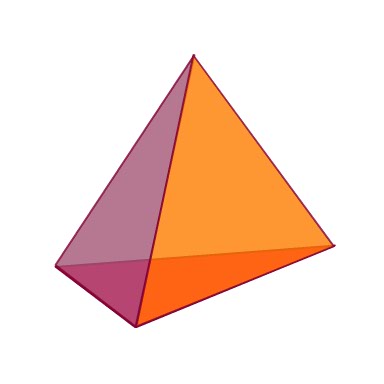
Now we are going to change from a polygon inscribed in a circle, to a pyramid inscribed in a Cone to explore the cones volume. We are also going to move back to a polygon with a more manageble number of side - for this example I am going to use a square. A square pyramid is also the most common pyramid used in elementary math
 |
The figure to the left is a square pyramid. Because it is regular, its lateral faces are all Isosceles Triangles. The line segment EF is drawn from the vertex of the pyramid perpendicular to its base. This is called the 'Slant Height' of the pyramid and is also perpendicular the height of the triangle. I will refer to this line as t. The area of each of the Isosceles Triangular faces is: The length of one side of the polygon multiplied by the slant height, all divided by two. Or .... ts/2 Where t is the slant height and s is the length of one side of the polygon base. |
We have now establised a formula for the area of JUST ONE of the triangular faces of a Regular Pyramid. But Now we need to establish a formula for a pyramid created by a polygon with ANY NUMBER OF SIDES.
I am going to say that the polygon base of our pyramid has
X number of sides.
So now we can say that the area of all the triangular faces added together is:
(x)ts/2
 |
We know that 's' the length of one side of the polygon, multiplied by 'x' the number of sides of the polygon, is in fact the Perimeter (P) of the polygon. So the above equation of the total area of all the triangles can be rewritten as; The Perimeter of the base multiplied by the Slant height. |
Let's return to the cone!
 |
We established that the Lateral surface area of a pyramid is the (perimeter of base x slant height) all divided by 2. We established that if you continue to increase the number of sides of the polygon, you will ultimately reach a circle, so .. |
Rather than using P for the perimeter of the polygon, we use C for the circumference of the base of the cone to get:
We know C = 2 Pi r
By Substituting 2 Pi r for C in the above equation we arrive at the formula:

The Total Surface Area is the Lateral Surface Area + the area of the circular base:
Pir2Once your student understands these concepts, you may also be interested in checking out my explanation of the volume of a cone.
I am sure you will find all the information and worksheets you need here, however if there is anything you cannot find please don't hesitate to contact me or simply visit the MathMomentumCommunity and join the conversation!
I love to hear from my readers, and with a little feedback and a few suggestions I can make this a great resource for parents, teachers and tutors alike.
Be sure to explore everything on this site starting at the home page.